1 Die geometrischen Bücher I bis IV
1.1 Betrachtung des Inhalts der Bücher I bis IV
1.2 Aufdeckung von inhaltlichen Schwächen
1.2.1 Exkurs: Der Perfektionismus im Axiomensystem
1.2.2 Das Axiomensystem Euklids
1.2.3 Das "Parallelenpostulat"
2 Die Entwicklung einer "neuen" Geometrie:
Auf dem Wege zur nichteuklidischen Geometrie
2.1 Das Saccheri-Viereck und seine Bedeutung
2.2 Die Vertreter der hyperbolischen Geometrie
2.2.1 C.F. Gauß und die nichteuklidische Geometrie
2.2.2 J. Bolyai und N.I. Lobatschewskij und die nichteuklididsche Geometrie
2.3 B. Riemann als Begründer der elliptischen Geometrie
2.4 Das Erlanger Programm
2.5 Die Axiomatisierung durch David Hilbert

Felix Klein
Aus Kleins Arbeiten ergab sich folgende Terminologie:
� hyperbolische Geometrie (Gauß, Bolyai, Lobatschewskij): In ihr schneidet jede Gerade den als Absolutum dienenden Kegelschnitt in zwei reellen Punkten (analog schneidet jede Hyperbel die Gerade im Unendlichen in zwei Punkten);
� elliptische Geometrie (Riemann): Sie bildet eine Analogie zwischen der gewöhnlichen Ellipse, die einen leeren Durchschnitt mit der Ferngeraden hat, und den Geraden, die keine gemeinsamen reellen Punkte mit den Kegelschnitten haben;
� parabolische Geometrie (Euklid): Ihre Geraden schneiden die zugrunde liegenden Kegelschnitte (u.a. die Parabel) in einem einzigen reellen Punkt.
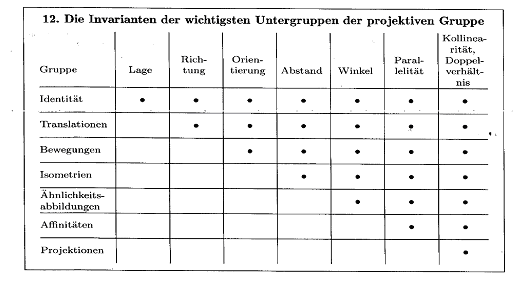
Abbildung 10
Zur vorherigen Seite Vorheriges Kapitel Nächstes Kapitel